G2solve3arc Class Reference

Clothoids: G2lib::G2solve3arc Class Reference

Clothoids

#include <ClothoidList.hxx>

Public Member Functions
void	set_tolerance (real_type tol)

void	set_max_iter (integer miter)

int	build (real_type x0, real_type y0, real_type theta0, real_type kappa0, real_type x1, real_type y1, real_type theta1, real_type kappa1, real_type Dmax=0, real_type dmax=0)

int	build_fixed_length (real_type s0, real_type x0, real_type y0, real_type theta0, real_type kappa0, real_type s1, real_type x1, real_type y1, real_type theta1, real_type kappa1)

ClothoidCurve const &	S0 () const

ClothoidCurve const &	S1 () const

ClothoidCurve const &	SM () const

real_type	total_length () const

real_type	theta_total_variation () const

real_type	curvature_total_variation () const

real_type	integral_curvature2 () const

real_type	integral_jerk2 () const

real_type	integral_snap2 () const

real_type	theta_min_max (real_type &thMin, real_type &thMax) const

real_type	delta_theta () const

real_type	curvature_min_max (real_type &kMin, real_type &kMax) const

real_type	theta (real_type s) const

real_type	theta_D (real_type s) const

real_type	theta_DD (real_type s) const

real_type	theta_DDD (real_type s) const

real_type	X (real_type s) const

real_type	Y (real_type s) const

real_type	x_begin () const

real_type	y_begin () const

real_type	kappa_begin () const

real_type	theta_begin () const

real_type	x_end () const

real_type	y_end () const

real_type	kappa_end () const

real_type	theta_end () const

void	eval (real_type s, real_type &theta, real_type &kappa, real_type &x, real_type &y) const

void	eval (real_type s, real_type &x, real_type &y) const

void	eval_D (real_type s, real_type &x_D, real_type &y_D) const

void	eval_DD (real_type s, real_type &x_DD, real_type &y_DD) const

void	eval_DDD (real_type s, real_type &x_DDD, real_type &y_DDD) const

void	eval_ISO (real_type s, real_type offs, real_type &x, real_type &y) const

void	eval_ISO_D (real_type s, real_type offs, real_type &x_D, real_type &y_D) const

void	eval_ISO_DD (real_type s, real_type offs, real_type &x_DD, real_type &y_DD) const

void	eval_ISO_DDD (real_type s, real_type offs, real_type &x_DDD, real_type &y_DDD) const

void	rotate (real_type angle, real_type cx, real_type cy)

void	translate (real_type tx, real_type ty)

void	reverse ()

void	save (ostream_type &stream) const
	save clothoid list of a file stream

Friends
ostream_type &	operator<< (ostream_type &stream, ClothoidCurve const &c)

Detailed Description

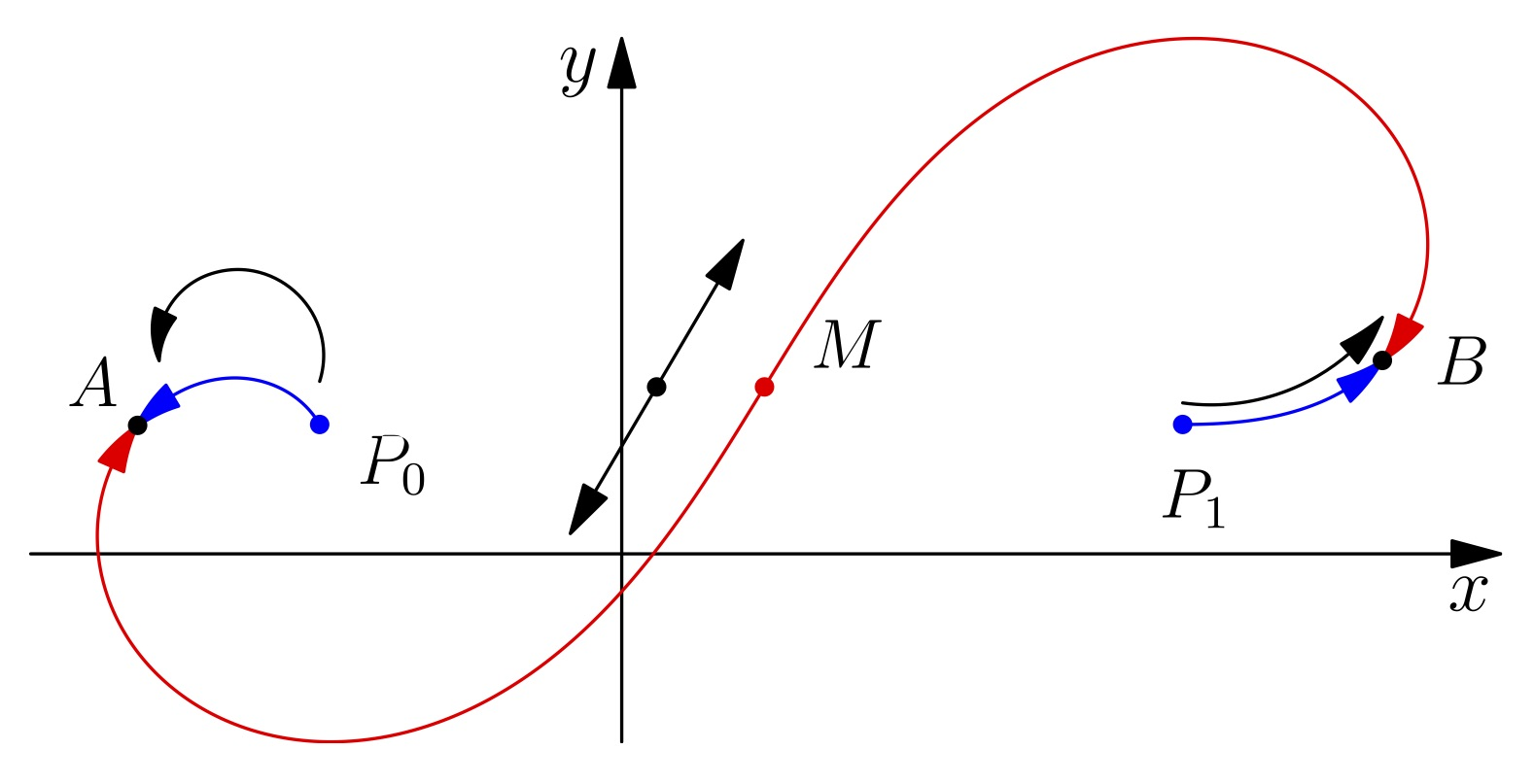
Construct a piecewise clothoids \( G(s) \) composed by 3 clothoid and one line segment that solve the \( G^2 \) problem

match

\[ \begin{array}{ll} \textrm{endpoints:}\quad& \left\{ \begin{array}{r@{~}c@{~}l} G(0) &=& \mathbf{p}_0 \\[0.5em] G(L) &=& \mathbf{p}_1 \end{array} \right. \\[1em] \textrm{angles:}\quad& \left\{ \begin{array}{r@{~}c@{~}l} \theta(0) &=& \theta_0 \\[0.5em] \theta(L) &=& \theta_1 \end{array} \right. \\[1em] \textrm{curvature:}\quad& \left\{ \begin{array}{r@{~}c@{~}l} \kappa(0) &=& \kappa_0 \\[0.5em] \kappa(L) &=& \kappa_1 \end{array} \right. \end{array} \]

Reference

The solution algorithm is described in

E.Bertolazzi, M.Frego, On the \( G^2 \) Hermite Interpolation Problem with clothoids Journal of Computational and Applied Mathematics, vol 341, pp. 99-116, 2018

'

Member Function Documentation

◆ build()

int G2lib::G2solve3arc::build	(	real_type	x0,
		real_type	y0,
		real_type	theta0,
		real_type	kappa0,
		real_type	x1,
		real_type	y1,
		real_type	theta1,
		real_type	kappa1,
		real_type	Dmax = 0,
		real_type	dmax = 0 )

Compute the 3 arc clothoid spline that fit the data

Parameters

[in]	x0	initial `x` position
[in]	y0	initial `y` position
[in]	theta0	initial angle
[in]	kappa0	initial curvature
[in]	x1	final `x` position
[in]	y1	final `y` position
[in]	theta1	final angle
[in]	kappa1	final curvature
[in]	Dmax	rough desidered maximum angle variation, if 0 computed automatically
[in]	dmax	rough desidered maximum angle divergence from guess, if 0 computed automatically

Returns: number of iteration, -1 if fails

◆ build_fixed_length()

int G2lib::G2solve3arc::build_fixed_length	(	real_type	s0,
		real_type	x0,
		real_type	y0,
		real_type	theta0,
		real_type	kappa0,
		real_type	s1,
		real_type	x1,
		real_type	y1,
		real_type	theta1,
		real_type	kappa1 )

Compute the 3 arc clothoid spline that fit the data

Parameters

[in]	s0	length of the first segment
[in]	x0	initial `x` position
[in]	y0	initial `y` position
[in]	theta0	initial angle
[in]	kappa0	initial curvature
[in]	s1	length of the last segment
[in]	x1	final `x` position
[in]	y1	final `y` position
[in]	theta1	final angle
[in]	kappa1	final curvature

Returns: number of iteration, -1 if fails

◆ curvature_min_max()

real_type G2lib::G2solve3arc::curvature_min_max	(	real_type &	kMin,
		real_type &	kMax ) const

Parameters

[out]	kMin	minimum curvature in the 3 arc \( G^2 \) fitting curve
[out]	kMax	maximum curvature in the 3 arc \( G^2 \) fitting curve

Returns: the difference of kMax and kMin

◆ curvature_total_variation()

real_type G2lib::G2solve3arc::curvature_total_variation ( ) const

inline

Returns: get the total curvature variation of the 3 arc \( G^2 \) fitting

◆ delta_theta()

real_type G2lib::G2solve3arc::delta_theta ( ) const

inline

Return the difference of maximum-minimum angle in the 3 arc \( G^2 \) fitting curve

◆ eval() [1/2]

void G2lib::G2solve3arc::eval	(	real_type	s,
		real_type &	theta,
		real_type &	kappa,
		real_type &	x,
		real_type &	y ) const

Compute parameters of 3 arc clothoid at curvilinear coordinate \(s\)

Parameters

[in]	s	curvilinear coordinate of where curve is computed
[out]	theta	the curve angle
[out]	kappa	the curve curvature
[out]	x	the curve \(x\)-coordinate
[out]	y	the curve \(y\)-coordinate

◆ eval() [2/2]

void G2lib::G2solve3arc::eval	(	real_type	s,
		real_type &	x,
		real_type &	y ) const

x and \(y\)-coordinate at curvilinear coordinate \(s\)

◆ eval_D()

void G2lib::G2solve3arc::eval_D	(	real_type	s,
		real_type &	x_D,
		real_type &	y_D ) const

x and \(y\)-coordinate derivative at curvilinear coordinate \(s\)

◆ eval_DD()

void G2lib::G2solve3arc::eval_DD	(	real_type	s,
		real_type &	x_DD,
		real_type &	y_DD ) const

x and \(y\)-coordinate second derivative at curvilinear coordinate \(s\)

◆ eval_DDD()

void G2lib::G2solve3arc::eval_DDD	(	real_type	s,
		real_type &	x_DDD,
		real_type &	y_DDD ) const

x and \(y\)-coordinate third derivative at curvilinear coordinate \(s\)

◆ eval_ISO()

void G2lib::G2solve3arc::eval_ISO	(	real_type	s,
		real_type	offs,
		real_type &	x,
		real_type &	y ) const

x and \(y\)-coordinate at curvilinear coordinate \(s\) with offset

◆ eval_ISO_D()

void G2lib::G2solve3arc::eval_ISO_D	(	real_type	s,
		real_type	offs,
		real_type &	x_D,
		real_type &	y_D ) const

x and \(y\)-coordinate derivative at curvilinear coordinate \(s\) with offset

◆ eval_ISO_DD()

void G2lib::G2solve3arc::eval_ISO_DD	(	real_type	s,
		real_type	offs,
		real_type &	x_DD,
		real_type &	y_DD ) const

x and \(y\)-coordinate second derivative at curvilinear coordinate \(s\) with offset

◆ eval_ISO_DDD()

void G2lib::G2solve3arc::eval_ISO_DDD	(	real_type	s,
		real_type	offs,
		real_type &	x_DDD,
		real_type &	y_DDD ) const

x and \(y\)-coordinate third derivative at curvilinear coordinate \(s\) with offset

◆ integral_curvature2()

real_type G2lib::G2solve3arc::integral_curvature2 ( ) const

inline

Returns: get the integral of the curvature squared of the 3 arc \( G^2 \) fitting

◆ integral_jerk2()

real_type G2lib::G2solve3arc::integral_jerk2 ( ) const

inline

Returns: get the integral of the jerk squared of the 3 arc \( G^2 \) fitting

◆ integral_snap2()

real_type G2lib::G2solve3arc::integral_snap2 ( ) const

inline

Returns: get the integral of the snap squared of the 3 arc \( G^2 \) fitting

◆ kappa_begin()

real_type G2lib::G2solve3arc::kappa_begin ( ) const

inline

Return initial curvature of the 3 arc clothoid

◆ kappa_end()

real_type G2lib::G2solve3arc::kappa_end ( ) const

inline

Return final curvature of the 3 arc clothoid

◆ reverse()

void G2lib::G2solve3arc::reverse ( )

inline

Reverse curve parameterization

◆ rotate()

void G2lib::G2solve3arc::rotate	(	real_type	angle,
		real_type	cx,
		real_type	cy )

inline

Rotate curve by angle \( \theta \) centered at point \( (c_x,c_y) \)

Parameters

[in]	angle	angle \( \theta \)
[in]	cx	\( c_x \)
[in]	cy	\( c_y \)

◆ S0()

ClothoidCurve const & G2lib::G2solve3arc::S0 ( ) const

inline

Returns: get the first clothoid for the 3 arc \( G^2 \) fitting

◆ S1()

ClothoidCurve const & G2lib::G2solve3arc::S1 ( ) const

inline

Returns: get the last clothoid for the 3 arc \( G^2 \) fitting

◆ set_max_iter()

void G2lib::G2solve3arc::set_max_iter ( integer miter )

Fix maximum number of iteration for the \( G^2 \) problem

◆ set_tolerance()

void G2lib::G2solve3arc::set_tolerance ( real_type tol )

Fix tolerance for the \( G^2 \) problem

◆ SM()

ClothoidCurve const & G2lib::G2solve3arc::SM ( ) const

inline

Returns: get the middle clothoid for the 3 arc \( G^2 \) fitting

◆ theta()

real_type G2lib::G2solve3arc::theta ( real_type s ) const

Return angle as a function of curvilinear coordinate

◆ theta_begin()

real_type G2lib::G2solve3arc::theta_begin ( ) const

inline

Return initial angle of the 3 arc clothoid

◆ theta_D()

real_type G2lib::G2solve3arc::theta_D ( real_type s ) const

Return angle derivative (curvature) as a function of curvilinear coordinate

◆ theta_DD()

real_type G2lib::G2solve3arc::theta_DD ( real_type s ) const

Return angle second derivative (curvature derivative) as a function of curvilinear coordinate

◆ theta_DDD()

real_type G2lib::G2solve3arc::theta_DDD ( real_type s ) const

Return angle third derivative as a function of curvilinear coordinate

◆ theta_end()

real_type G2lib::G2solve3arc::theta_end ( ) const

inline

Return final angle of the 3 arc clothoid

◆ theta_min_max()

real_type G2lib::G2solve3arc::theta_min_max	(	real_type &	thMin,
		real_type &	thMax ) const

Parameters

[out]	thMin	minimum angle in the 3 arc \( G^2 \) fitting curve
[out]	thMax	maximum angle in the 3 arc \( G^2 \) fitting curve

Returns: the difference of thMax and thMin

◆ theta_total_variation()

real_type G2lib::G2solve3arc::theta_total_variation ( ) const

inline

Returns: get the total angle variation of the 3 arc \( G^2 \) fitting

◆ total_length()

real_type G2lib::G2solve3arc::total_length ( ) const

inline

Returns: get the length of the 3 arc \( G^2 \) fitting

◆ translate()

void G2lib::G2solve3arc::translate	(	real_type	tx,
		real_type	ty )

inline

Translate curve by \( (t_x,t_y) \)

◆ X()

real_type G2lib::G2solve3arc::X ( real_type s ) const

Return \(x\)-coordinate of the arc clothoid as a function of curvilinear coordinate

◆ x_begin()

real_type G2lib::G2solve3arc::x_begin ( ) const

inline

Return initial \(x\)-coordinate of the 3 arc clothoid

◆ x_end()

real_type G2lib::G2solve3arc::x_end ( ) const

inline

Return final \(x\)-coordinate of the 3 arc clothoid

◆ Y()

real_type G2lib::G2solve3arc::Y ( real_type s ) const

Return \(y\)-coordinate of the arc clothoid as a function of curvilinear coordinate

◆ y_begin()

real_type G2lib::G2solve3arc::y_begin ( ) const

inline

Return initial \(y\)-coordinate of the 3 arc clothoid

◆ y_end()

real_type G2lib::G2solve3arc::y_end ( ) const

inline

Return final \(y\)-coordinate of the 3 arc clothoid

Friends And Related Symbol Documentation

◆ operator<<

ostream_type & operator<<	(	ostream_type &	stream,
		ClothoidCurve const &	c )

friend

Print on strem the ClothoidCurve object

Parameters

stream	the output stream
c	an instance of `ClothoidCurve` object

Returns: the output stream

The documentation for this class was generated from the following files:

/Users/enrico/Ricerca/develop/PINS/pins-mechatronix/LibSources/submodules/Clothoids/src/Clothoids/ClothoidList.hxx
/Users/enrico/Ricerca/develop/PINS/pins-mechatronix/LibSources/submodules/Clothoids/src/ClothoidG2.cc
/Users/enrico/Ricerca/develop/PINS/pins-mechatronix/LibSources/submodules/Clothoids/src/ClothoidList.cc

G2solve3arc Class Reference

Public Member Functions

Friends

Detailed Description

Member Function Documentation

◆ build()

◆ build_fixed_length()

◆ curvature_min_max()

◆ curvature_total_variation()

◆ delta_theta()

◆ eval() [1/2]

◆ eval() [2/2]

◆ eval_D()

◆ eval_DD()

◆ eval_DDD()

◆ eval_ISO()

◆ eval_ISO_D()

◆ eval_ISO_DD()

◆ eval_ISO_DDD()

◆ integral_curvature2()

◆ integral_jerk2()

◆ integral_snap2()

◆ kappa_begin()

◆ kappa_end()

◆ reverse()

◆ rotate()

◆ S0()

◆ S1()

◆ set_max_iter()

◆ set_tolerance()

◆ SM()

◆ theta()

◆ theta_begin()

◆ theta_D()

◆ theta_DD()

◆ theta_DDD()

◆ theta_end()

◆ theta_min_max()

◆ theta_total_variation()

◆ total_length()

◆ translate()

◆ X()

◆ x_begin()

◆ x_end()

◆ Y()

◆ y_begin()

◆ y_end()

Friends And Related Symbol Documentation

◆ operator<<